Volume Around X Axis Calculator

Formulas to calculate the volume generated by revolving graphs of functions around one of the axes

Formula i - Disk effectually the ten axis

If f is a function such that f(x) ≥ 0 for all x in the interval [x ₁ , 10 _ii ], the volume of the solid generated by revolving, around the x axis, the region divisional past the graph of f, the x centrality (y = 0) and the vertical lines x = x ₁ and ten = _ii is given by the integral

Figure i. volume of a solid of revolution generated past rotating a triangle around the x centrality

Formula 2 - Washer effectually the 10 axis

If f and h are functions such that f(ten) ≥ h(ten) for all x in the interval [x _i , 10 ₂ ], the book of the solid generated by revolving, effectually the 10 centrality, the region bounded by the graphs of f and h, between x = 10 ₁ and x = x ₂ is given by the integral

\Big {\text{Book} = \color{red}{\int_{x_1}^{x_2} \pi [ f(10)^2 - h(x)^2 ] dx}}

Figure 2. book of a solid of revolution generated by rotating two curves around the ten axis

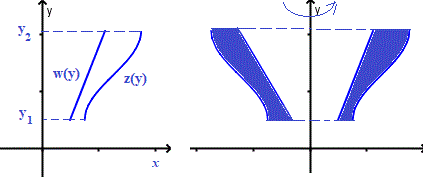
Formula three - Disk around the y axis

If z is a function of y such that x = z(y) and z(y)≥ 0 for all y in the interval [y1 , y2], the volume of the solid generated by revolving, around the y axis, the region bounded by the graph of z, the y axis (x = 0) and the horizontal lines y = y1 and y = y2 is given by the integral

\LARGE { \text{Volume} = \color{ruby}{\int_{y_1}^{y_2} \pi ( z(y) )^2 dy}}

Figure three. volume of a solid of revolution generated by rotating a bend effectually the y axis

Formula 4 - Washer around the y axis

If z and west are functions of y such that z(y) ≥ westward(y) for all y in the interval [ y1 , y2 ], the volume of the solid generated past revolving the region bounded by the graphs of z and west, between y = y1 and y = y2, around the y axis , is given by the integral

\LARGE { \text{Book} = \color{red}{\int_{y_1}^{y_2} \pi [ z(y)^ii - west(y)^2 ] dy}}

Effigy 4. volume of a solid of revolution generated by rotating two curves around the y axis

Examples to Find Volume of a Solid of Revolution Using Definite Integrals

Case 1

Notice the volume of the solid generated by revolving the region bounded by the graph of y = x, y = 0, 10 = 0 and x = two.(see figure below).

Figure 5. book of a solid of revolution generated by rotation of y = ten around x centrality

Solution to Case 1

We present ii methods

Method 1

This problem may exist solved using the formula for the volume of a right round cone.
volume = (one/3) π (radius) ² superlative
= (ane/3) π(2) ² 2
= 8π/3

Method 2

We now use definite integrals to detect the book defined above. If we let f(x) = x according to formula i above, the book is given by the definite integral

\text{Volume} = \int_{x_1}^{x_2} \pi f(10)^2 dx = \int_{0}^{2} \pi 10^two dx = \left [\pi x^3 / 3 \correct ]_0^ii = viii\pi/three

The outset method works because y = x is a linear role and the volume generated is that of a right circular cone , however the second method work for shapes other than cones and will be used in the examples beneath.

Example 2

Find the book of the solid generated by revolving the semicircle y = √ (r ² - x ² ) around the 10 axis, radius r > 0.

Solution to Example 2

Figure 6. book of a solid of revolution generated by the rotation of a semi circumvolve around ten axis

The graph of y = √(r ² - ten ²) is shown above and y ≥ 0 from x = -r to 10 = r. The volume is given by formula i as follows

\text{Volume} = \int_{x_1}^{x_2} \pi f(x)^2 dx = \int_{-r}^{r} \pi (\sqrt{r^two - ten^two})^2 dx = \int_{-r}^{r} \pi (r^2 - x^2) dx \\\\\\ = \pi\left [r^2 x - 10^three/3 \right ]_{-r}^r = \pi\left [ (r^three - r^3/iii) - (-r^3 + r^three/3) \right ] = \dfrac{4}{3} \pi r^3

This is the very well known formula for the book of the sphere. If you lot revolve a semi circle of radius r around the x axis, it will generate a sphere of radius r.

Instance iii

Find the book of the solid generated past revolving the shaded (cherry-red) region almost the y centrality.

Figure seven. volume of a solid of revolution generated by a triangle around y centrality

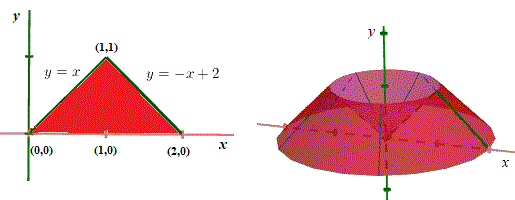
Solution to Example 3

The shaded (reddish) region is bounded by the ten axis, the line that passes through the points (0,0) and (ane,1) and has the equation y = x, and the line that passes through the points (1,one) and (2,0) and has the equation y = -x + two. Since the solid is generated past revolving through the y axis, we will apply formula iv given higher up to detect the volume as follows. The limits of integration are y = 0 and y = one

\text{Volume} = \int_{y_1}^{y_2} \pi [z(y)^2 - due west(y)^2] dy

Solve y = - x + 2 for ten
10 = z(y) = - y + 2
Solve y = x for 10
x = westward(y) = y
Substitute in the formula for the volume to obtain

\text{Volume} = \int_{0}^{1} \pi [ (-y+two)^2 - y^2] dy \\ = \int_{0}^{1} \pi [ - 4 y + 4] dy \\ = \pi \left [-2y^2+4y \right ]_0^ane = ii\pi

Case four

Notice the volume of the solid generated past the rotation of curves y = 1 + x ^two and y = √ten, around the x axis and limited to the left past x = 0 and to the right by x = two.

Figure eight. volume of a solid of revolution generated by the rotation of curves y = ane + x² and y = √x, around the 10 centrality

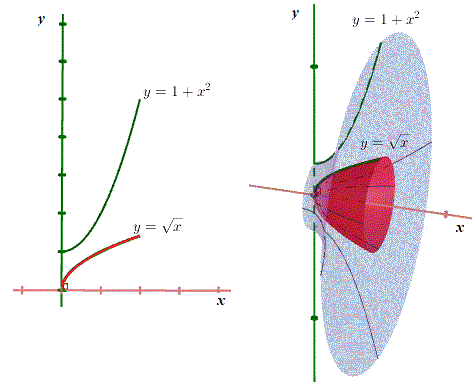
Solution to Case 4

We now utilize formula 2 above, washers with integration along the x axis. The limits of integration are x = 0 and 10 = ii. Let f(x) = 1 + xⁱⁱ and h(x) = √10

\text{Volume} = \int_{x_1}^{x_2} \pi [ f(x)^two - h(10)^2 ] dx = \int_{0}^{2} \pi [ (i+x^two)^2 - (\sqrt x)^2 ]dx\\ \\ = \pi \int_{0}^{ii} [ 1+x^4+2x^two - 10 ] dx = \pi \left [ x^5/5 + 2x^3/3 - x^2/2 + x \right]_0^ii = 176\pi / 15

Example 5

Find the volume of the torus generated when the circle with center at (0,R) and radius r is rotated around the 10 axis.

Figure nine. Torus generated when the circle with center at (0,R) and radius r is rotated around the x centrality

Solution to Example 5

The equation of the circle is given by
x ² + (y - R) ² = r ²
Solve the higher up equation for y to obtain two solutions each for i semicircle
y = R + √(r ² - ten ⁱⁱ ) , upper semi circle , and y = R - √(r ^two - 10 ⁱⁱ ) , lower semi circle
The torus is generated by rotating the two halves semi circles the ten axis hence the employ of formula two given to a higher place to detect the book of the torus. Let f(x) = R + √(r ^two - 10 ²) and h(x) = R - √(r ² - x ²). Because of the symmetry of the circumvolve and therefore the torus with respect to the y axis, we integrate from x = 0 to x = r and then double the answer to find the full volume.

\text{Volume} = \int_{0}^{r} \pi [ f(x)^2 - h(x)^2 ] dx \\\\ = \pi \int_{0}^{r} [ (R + \sqrt(r^2 - ten^ii))^2 - (R - \sqrt(r^2 - 10^two))^2 ]dx \\\\ = 4 R \pi \int_{0}^{r} [ \sqrt(r^2 - x^2) ]dx = 4 R \pi (ane/2) \left [ x \sqrt{r^two-x^2} + r^two\arctan(\frac{10}{\sqrt{r^2-x^two}}) \correct ]_0^r\\\\ = 4 R \pi ( \pi r^ii / four) = {\pi}^2 R r^2

The total volume is twice the above, hence the volume of a torus is given by

\text{Volume} = 2 {\pi}^2 R r^ii

Exercises

(ane) Find the volume of the solid generated when the region betwixt the graphs of f(x) = ten ² + 2 and h(10) = x is revolved about the ten axis and over the interval [0,1].
(2) Find the volume generated when the finite region bounded by the curves y = x ³ , y = ten ² is revolved about the y axis.(hint: you need to find the points of intersections of the two curves)

Answers to To a higher place Exercises

(1) 26 Pi /five
(2) pi /10

More Links and References

Volume by Cylindrical Shells Method.
integrals and their applications in calculus.
Area nether a curve.
Area between 2 curves.

Volume Around X Axis Calculator,

Source: https://www.analyzemath.com/calculus/Integrals/volume_solid_1.html

Posted by: sanchezyournegand.blogspot.com

Share this post